Konsultasi Statistik Uji Korelasi

Analisis Uji korelasi merupakan teknik analisis yang termasuk dalam pengukuran hubungan yang digunakan untuk mengukur kekuatan hubungan antara dua variabel maupun lebih dari dua variabel atau beberapa variabel. Dari teknik pengukuran hubungan tersebut

terdapat dua teknik korelasi yang sangat populer sampai sekarang, yaitu Korelasi Pearson Product Moment dan Korelasi Rank Spearman.

Pengukuran hubungan tersebut yaitu untuk mengetahui kekuatan hubungan antara variabel atau beberapa variabel. Dua variabel atau beberapa variabel dikatakan berasosiasi jika perilaku variabel yang satu mempengaruhi variabel yang lain. Jika tidak terjadi pengaruh, maka kedua variabel tersebut disebut independen.

Dikutip dari sumber : Jonathan Sarwono

Berikut ini kita akan membahas mengenai perhitungan uji korelasi menggunakan aplikasi SPSS. 

Contoh kasus kita akan melakukan uji korelasi 4 variabel yaitu X1, X2, X3 dan Y, anggap saja kita telah mempunyai data tabulasi hasil kuesioner.

Untuk melakukan uji korelasi dengan aplikasi SPSS langkah selanjutnya adalah kita lakukan copy hanya kolom jumlah total dari masing-masing variabel mulai dari variabel X1, X2, X3 dan Y kemudian kita lakukan paste pada lembar kerja SPSS seperti berikut ini :

Langkah selanjutnya yaitu kita pilih menu Analyze > Correlate > Bivariate seperti pada gambar dibawah ini :

Maka akan tampil gambar seperti berikut ini :

Pindahkan variabel X1, X2, X3 dan Y ke sebelah kanan dibagian variables seperti gambar diatas, setelah itu kita klik tombol OK, maka akan tampil laporan/output sebagai berikut :

Dari hasil tabel diatas merupakan hubungan antara variabel independent, selanjutnya kita lakukan kembali analisis untuk mengetahui hubungan antara variabel independent dengan variabel Dependent dengan cara sebagai berikut :

Maka akan tampil sebagai berikut :

Pindahkan variabel Y ke sebelah kanan dibagian Dependent, dan pindahkan variabel X1, X2 dan X3 ke sebelah kanan dibagian Independent(s), dan klik tombol Statistics kemudian ceklis pada R squared change, maka akan tampil sebagai berikut :

Setelah itu kita klik tombol Continue dan klik tombol OK maka akan tampil gambar sebagai berikut :

Dari hasil output tabel diatas, maka langkah selanjutnya kita lakukan rekafitulasi hubungan antar variabel dalam hal ini antara variabel Independen dengan variabel Dependen sebagai berikut :

Mengacu pada hasil tersebut maka kita harus melihat tabel koefisiensi korelasi untuk dapat mengambil kesimpulan hubungan antar variabel tersebut, berikut tabel koefisien korelasi :

Penjelasan :

Berdasarkan hasil tabel diatas, diketahui bahwa besarnya hubungan antara variabel (X1) dengan (X2) yang dihitung dengan koefisien korelasi adalah sebesar 0.635 atau (r X1 X2= 0.635). Hal ini menunjukan bahwa hubungan antara kedua variabel tersebut bersifat tinggi dan searah. 

Uji signifikansi koefisien korelasi menghasilkan angka Sig. sebesar 0.000 dan lebih kecil dari pada α = 0.05. (Sig. = 0.000 < 0.05). Maka artinya Ho ditolak dan dapat disimpulkan bahwa variabel (X1) berhubungan secara signifikan dengan variabel (X2).

Berdasarkan hasil tabel diatas, diketahui bahwa besarnya hubungan antara variabel (X1) dengan (X3) yang dihitung dengan koefisien korelasi adalah sebesar 0.576 atau (r X1 X3 = 0.576). Hal ini menunjukan bahwa hubungan antara kedua variabel tersebut bersifat sedang dan searah.

Uji signifikansi koefisien korelasi menghasilkan angka Sig. sebesar 0.000 dan lebih kecil daripada α= 0.05. (Sig. = 0.000 < 0.05). Maka artinya Ho ditolak dan dapat disimpulkan bahwa variabel (X1) berhubungan secara signifikan dengan variabel (X3).

Berdasarkan hasil tabel diatas, diketahui bahwa besarnya hubungan antara variabel (X2) dengan (X3) yang dihitung dengan koefisien korelasi adalah sebesar 0.612 atau (r X2 X3= 0.612). Hal ini menunjukan bahwa hubungan antara kedua variabel tersebut bersifat tinggi dan searah. 

Uji signifikansi koefisien korelasi menghasilkan angka Sig. sebesar 0.000 dan lebih kecil daripada α= 0.05. (Sig. = 0.000 < 0.05). Maka artinya Ho ditolak dan dapat disimpulkan bahwa variabel (X2) berhubungan secara signifikan dengan variabel (X3).

Berdasarkan hasil tabel diatas, diketahui bahwa besarnya hubungan antara variabel (X1) dengan (Y) yang dihitung dengan koefisien korelasi adalah sebesar 0.806 atau (r X1 Y= 0.806). Hal ini menunjukan bahwa hubungan antara kedua variabel tersebut bersifat sangat tinggi dan searah. 

Uji signifikansi koefisien korelasi menghasilkan angka Sig. sebesar 0.000 dan lebih kecil daripada α= 0.05. (Sig. = 0.000 < 0.05). Maka artinya Ho ditolak dan dapat disimpulkan bahwa variabel (X1) berhubungan secara signifikan dengan variabel (Y).

Berdasarkan hasil tabel diatas, diketahui bahwa besarnya hubungan antara variabel (X2) dengan (Y) yang dihitung dengan koefisien korelasi adalah sebesar 0.811 atau (r X2 Y= 0.811). Hal ini menunjukan bahwa hubungan antara kedua variabel tersebut bersifat sangat tinggi dan searah.

Uji signifikansi koefisien korelasi menghasilkan angka Sig. sebesar 0.000 dan lebih kecil daripada α= 0.05. (Sig. = 0.000 < 0.05). Maka artinya Ho ditolak dan dapat disimpulkan bahwa variabel (X2) berhubungan secara signifikan dengan variabel (Y).

Berdasarkan hasil tabel diatas, diketahui bahwa besarnya hubungan antara variabel (X3) dengan (Y) yang dihitung dengan koefisien korelasi adalah sebesar 0.800 atau (r X3 Y= 0.800). Hal ini menunjukan bahwa hubungan antara kedua variabel tersebut bersifat sangat tinggi dan searah. 

Uji signifikansi koefisien korelasi menghasilkan angka Sig. sebesar 0.000 dan lebih kecil daripada α= 0.05. (Sig. = 0.000 < 0.05). Maka artinya Ho ditolak dan dapat disimpulkan bahwa variabel (X3) berhubungan secara signifikan dengan variabel (Y).

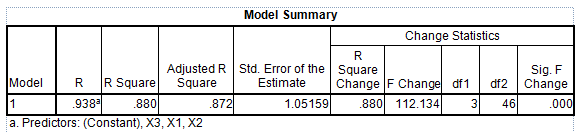
Berdasarkan hasil tabel diatas, diketahui bahwa besarnya korelasi antara variabel (X1), (X2), (X3) secara simultan terhadap variabel (Y) yang dihitung dengan koefisien korelasi adalah sebesar 0.938. Hal ini menunjukan bahwa hubungan antara variabel tersebut bersifat sangat tinggi dan searah. 

Uji signifikansi koefisien korelasi menghasilkan angka Sig. sebesar 0.000 dan lebih kecil daripada α= 0.05. (Sig. = 0.000 < 0.05). Maka artinya Ho ditolak dan dapat disimpulkan bahwa variabel (X1),(X2) dan (X3) secara simultan terhadap variabel (Y).

Demikian pembahasan mengenai analisis uji korelasi menggunakan SPSS, semoga tulisan kecil ini dapat bermanfaat dan membantu mahasiswa khususnya yang sedang melakukan penelitian berkaitan dengan Skripsi maupun Tesis.

Jika anda membutuhkan jasa perhitungan dari kami silakan isi Form Jasa atau dapat mengunjungi Facebook kami.